Dual Graphs of Planar Graphs

:::note Reference https://en.wikipedia.org/wiki/Dual_graph :::

A proof for Euler’s characteristic i.e. $F + V - E = 2$

:::info Note Note that for polyhedra, they can be reduced to planar graphs by considering one face of the polyhedra as the region outside the planar graph. :::

Planar Graph and its dual	Spanning trees (called Interdigitating trees in this context)

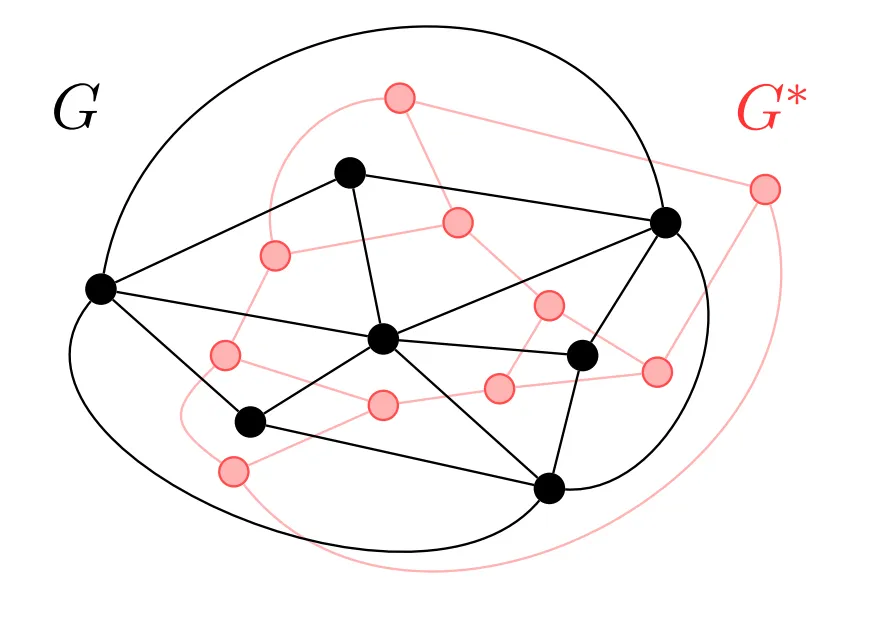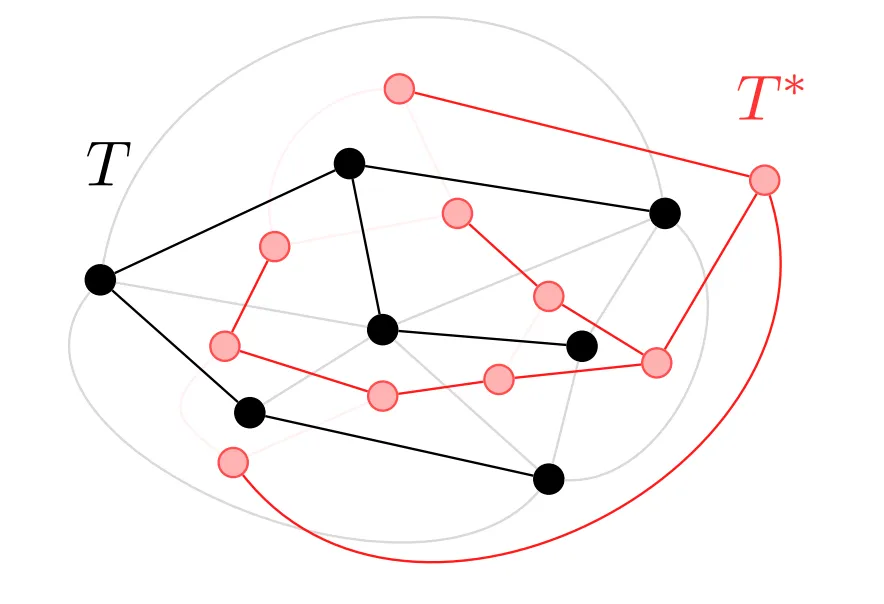By cut-cycle duality, if a set $S$ of edges in a planar graph $G$ is acyclic (has no cycles), then the set of edges dual to $S$ has no cuts, from which it follows that the complementary set of dual edges (the duals of the edges that are not in $S$) forms a connected subgraph. Symmetrically, if $S$ is connected, then the edges dual to the complement of $S$ form an acyclic subgraph. Therefore, when $S$ has both properties – it is connected and acyclic – the same is true for the complementary set in the dual graph. That is, each spanning tree of $G$ is complementary to a spanning tree of the dual graph, and vice versa. Thus, the edges of any planar graph and its dual can together be partitioned (in multiple different ways) into two spanning trees, one in the primal and one in the dual, that together extend to all the vertices and faces of the graph but never cross each other.

This partition of the edges and their duals into two trees leads to a simple proof of Euler’s formula $V - E + F = 2$ for planar graphs with $V$ vertices, $E$ edges, and $F$ faces. Any spanning tree and its complementary dual spanning tree partition the edges into two subsets of $V - 1$ and $F - 1$ edges respectively, and adding the sizes of the two subsets gives the equation

$$E = (V - 1) + (F - 1)$$

which may be rearranged to form Euler’s formula.