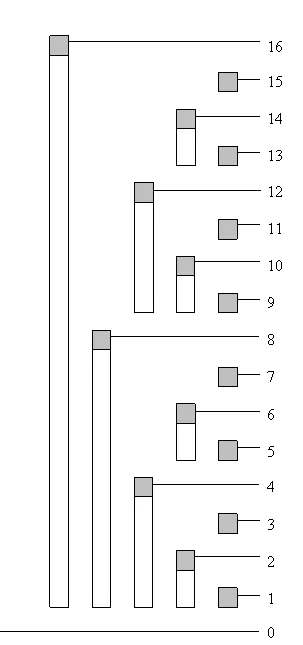Fenwick Tree / BIT

:::info Name Alias

Fenwick Tree
Binary Indexed Tree (BIT) :::

:::note Indexing

Zero-based indexing: x = (x & (x + 1)) - 1 and x |= (x + 1)
One-based indexing: x -= (x & -x) and x += (x & -x) :::

template<typename T> class FenwickTree {
private:
    std::vector<T> bit;

public:
    FenwickTree(int32_t size) { this->reset(size); }
    void reset(int32_t size) { bit.assign(size, 0); }
    T sum(int32_t l, int32_t r) const { return sum(r) - sum(l - 1); }

    T sum(int32_t x) const {
        T sum = 0;
        for (; x >= 0; x = (x & (x + 1)) - 1) sum += bit[x];
        return sum;
    }

    void add(int32_t x, int32_t value) {
        int32_t n = static_cast<int32_t>(bit.size());
        for (; x < n; x |= (x + 1)) bit[x] += value;
    }
};

Fenwick Tree in n-dimensions

template<typename T> class FenwickTree2D {
private:
    std::vector<std::vector<T>> bit;

public:
    FenwickTree2D(int32_t size) { this->reset(size); }
    void reset(int32_t size) { bit.assign(size, 0); }

    T sum(int32_t a, int32_t b) const {
        T sum = 0;
        for (int32_t x = a; x >= 0; x = (x & (x + 1)) - 1)
            for (int32_t y = b; y >= 0; y = (y & (y + 1)) - 1)
                sum += bit[x][y];
        return sum;
    }

    void add(int32_t a, int32_t b, int32_t value) {
        int32_t n = static_cast<int32_t>(bit.size());
        for (int32_t x = a; x < n; x |= (x + 1))
            for (int32_t y = b; y < n; y |= (y + 1))
                bit[x][y] += value;
    }
};